Cách tính diện tích hình phẳng, thể tích vật thể bằng tích phân đơn giản

Bạn đã bao giờ tự hỏi về cách tính diện tích hình phẳng và thể tích vật thể một cách đơn giản nhất chưa? Đây không chỉ là một khía cạnh quan trọng của tích phân mà còn là kiến thức cần thiết trong chương trình toán phổ thông. Vậy tại sao diện tích hình phẳng lại quan trọng đến vậy? Làm thế nào để giải các dạng bài tập liên quan đến tính diện tích hình phẳng một cách hiệu quả nhất?

Hãy cùng Laginhi.com khám phá và tổng hợp kiến thức sâu rộng về cách tính diện tích hình phẳng và thể tích vật thể trong bài viết dưới đây. Đừng bỏ lỡ cơ hội trau dồi kiến thức và nâng cao kỹ năng giải bài tập của mình!

Bạn đang xem: Cách tính diện tích hình phẳng, thể tích vật thể bằng tích phân đơn giản

Hiểu rõ về Diện Tích Hình Phẳng

Diện tích hình phẳng là một khái niệm quan trọng trong toán học, dùng để đo lường kích thước của các hình học trong không gian hai chiều. Đơn vị đo diện tích thường được thể hiện bằng mét vuông (m²), centimet vuông (cm²), kilômét vuông (km²),…

Ứng dụng của diện tích hình phẳng rất đa dạng trong nhiều lĩnh vực như xây dựng, đo lường, hình học, khoa học tự nhiên và kỹ thuật. Ví dụ, trong xây dựng và kiến trúc, diện tích mặt sàn và diện tích bề mặt đóng vai trò quan trọng. Trên thảo nguyên, diện tích đất trồng và đất canh tác cũng được tính bằng diện tích hình phẳng.

Có thể bạn quan tâm:

• Mét vuông đổi ra mét bằng bao nhiêu? Có đổi được không?
• Cách đổi inch sang mét một cách chính xác và nhanh chóng bằng công cụ
• 1 độ bằng bao nhiêu phút, giây, radian? Cách chuyển đổi đơn vị độ (góc)

Xem thêm : Rác thải nhựa là gì? Thực trạng, tác hại, biện pháp phòng ngừa

Tính diện tích hình phẳng là một ứng dụng quan trọng của tích phân trong chương trình toán phổ thông. Vậy diện tích hình phẳng là gì? Các dạng bài tập tìm diện tích hình phẳng? Cách tìm diện tích hình phẳng như nào? Trong bài viết dưới đây, chúng ta sẽ cùng tìm hiểu kiến thức về diện tích hình phẳng.

Câu hỏi Thường gặp (FAQs)

1. Diện tích hình phẳng là khái niệm gì?

   • Diện tích hình phẳng là một khái niệm trong toán học, đơn vị đo lường diện tích của một hình học nằm trong mặt phẳng hai chiều và thường được đo bằng mét vuông (m²), centimet vuông (cm²), kilômét vuông (km²),…

2. Diện tích hình phẳng được ứng dụng trong những lĩnh vực nào?

   • Diện tích hình phẳng được ứng dụng rộng rãi trong xây dựng, đo lường, hình học, khoa học tự nhiên, kỹ thuật, ví dụ như tính diện tích mặt sàn, diện tích bề mặt trong xây dựng và kiến trúc, hay diện tích đất trồng, đất canh tác trong nông nghiệp,…

3. Công thức tính diện tích hình phẳng cơ bản là gì?

   • Công thức cơ bản để tính diện tích hình phẳng bằng tích phân: S = ∫[ba] |f(x)|dx, với f(x) là hàm số liên tục trên đoạn [a;b].

4. Thể tích khối tròn xoay được tính như thế nào?

   • Thể tích khối tròn xoay được tính bằng π.∫[b;a] [f(x)]²dx, với f(x) là hàm số liên tục trên đoạn [a;b] khi quay hình phẳng giới hạn bởi các đường y=f(x) quanh trục Ox.

5. Làm thế nào để tìm diện tích hình phẳng giới hạn bởi hai hoặc ba hàm số?

   • Bước 1: Tìm hoành độ giao điểm của từng cặp đồ thị.
   • Bước 2: Tính diện tích hình phẳng bằng công thức: S= ∫[b;a] [g(x) – h(x)]dx – ∫[c;b] [f(x) – h(x)]dx.

6. Xem thêm : Vai trò của tầng Ozon? Nguyên nhân thủng tầng Ozon

   Cách tính diện tích hình phẳng được giới hạn bởi hai hàm số?

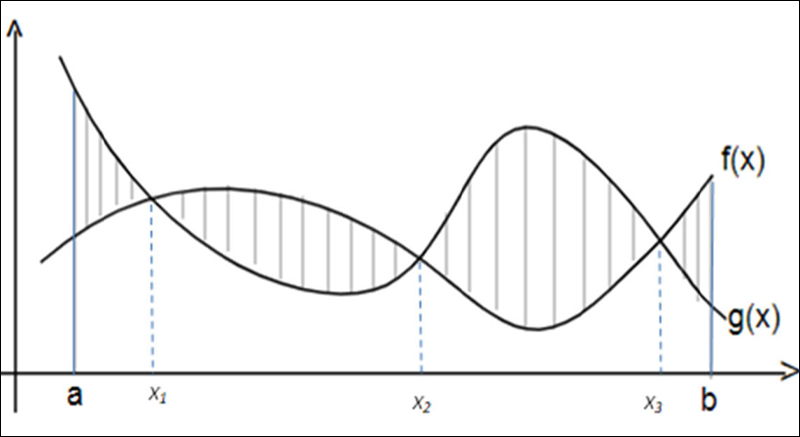
   • S=∫[ba] |f(x) − g(x)|dx, với f(x) và g(x) là hai hàm số liên tục trên đoạn [a;b].

7. Công thức tính diện tích hình phẳng mở rộng với hai đồ thị hàm số là gì?

   • Công thức: S=∫[ba] |f(x) − g(x)|dx, với f(x) và g(x) là hai hàm số liên tục trên đoạn [a;b].

8. Làm thế nào để tìm diện tích hình phẳng giới hạn bởi ba hàm số?

   • Ta cần tìm hoành độ giao điểm của từng cặp đồ thị, sau đó áp dụng công thức S= ∫[b;a] [g(x) – h(x)]dx – ∫[c;b] [f(x) – h(x)]dx.

9. Diện tích hình phẳng giới hạn bởi đồ thị hàm số f(x)= 2x + 1 và trục hoành trên đoạn [0;3] là bao nhiêu?

   • Diện tích này là 24 đơn vị diện tích.

Tóm tắt

Trên đây là một số kiến thức cơ bản về diện tích hình phẳng và cách tính toán liên quan. Hi vọng thông tin này sẽ giúp bạn hiểu rõ hơn về chủ đề này và áp dụng vào thực tế một cách linh hoạt. Để tìm hiểu thêm về các vấn đề liên quan, hãy truy cập trang web chính thức của chúng tôi.ớ.

Nguồn: https://laginhi.com
Danh mục: News