Kỹ thuật SEO hiệu quả sẽ đưa nội dung của bạn lên hàng đầu trang kết quả tìm kiếm. Với bài viết này về “Là Gì Nhỉ,” bạn cần sự chính xác và súc tích để thu hút độc giả ngay từ đầu.
Trong chương trình Toán lớp 6, lý thuyết về ước và bội chính là nền tảng quan trọng. Để giải các bài toán liên quan, hiểu rõ về khái niệm này là không thể thiếu. Vậy nên, hãy cùng LaGiNhi khám phá sâu hơn về ý nghĩa của ước và bội cũng như cách áp dụng chúng vào những dạng toán cụ thể.
Bạn đang xem: Lý thuyết ước và bội: Cách tìm ước và bội của một số (Toán 6)
Hãy để chúng tôi dẫn dắt bạn qua hành trình tìm hiểu đầy thú vị về lý thuyết ước và bội trong Toán 6. Đừng bỏ lỡ cơ hội được khám phá và hiểu rõ hơn về chủ đề hấp dẫn này!
Ước và bội là khái niệm gì?
Trong toán học, ước và bội thường được hiểu như sau:
Giả sử chúng ta có hai số tự nhiên a và b. Khi số a có thể chia hết cho số b mà không dư thì chúng ta nói:
- a là bội của b
- b là ước của a
Ngoài ra, chúng ta còn có tập hợp ước của số a được ký hiệu là Ư(a) và tập hợp bội của số b được ký hiệu là B(b).
Ví dụ: Khi số 12 chia hết cho 3 => 12 là bội của 3 và 3 là ước của 12.
- Ư(12) = {1; 2; 3; 4; 6; 12}
- B(3) = {3; 6; 9; 12; 15;…; 3k}

Cách tìm ước số
Khi muốn xác định ước số của một số tự nhiên a (với a>1), bạn có thể thực hiện theo hướng dẫn dưới đây: Tiến hành lần lượt chia a cho các số tự nhiên từ 1 đến a. Khi đó, nếu a chia hết cho một số nào đó thì số đó được coi là ước của a.
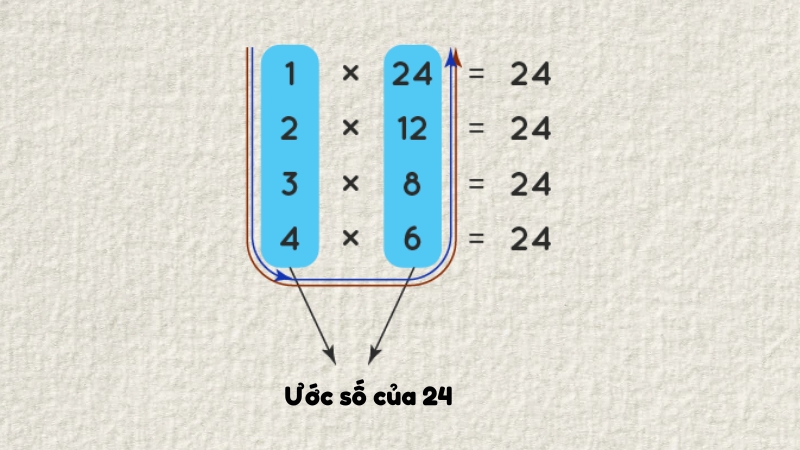
Ví dụ: Hãy tìm các ước của số 24.
Bạn tiến hành chia lần lượt 24 cho 1, 2, 3, 4,… cho đến 24. Kết quả, số 24 chia hết cho các số 1, 2, 3, 4, 6, 8, 12, 24.
Do đó, ta có: Ư (24) = {1, 2, 3, 4, 6, 8, 12, 24}.
Làm thế nào để xác định bội số
Để xác định bội số của một số tự nhiên a (với a≠0), bạn có thể áp dụng quy tắc sau đây: nhân số đó với 0, 1, 2,… Các kết quả thu được được gọi là các bội số k trong đó k thuộc tập số tự nhiên.
Ví dụ: Để tìm tập hợp các bội số của số 5 nhỏ hơn 20, bạn thực hiện việc nhân 5 lần lượt với 0, 1, 2,… cho đến khi nhận được bội số cuối cùng nhỏ hơn 20. Do đó, tập hợp các bội số của số 5 là:
=> B (5) = {0;5;10;15}
Loại 1: Xác định số là ước, bội của một số đã cho
Để giải dạng bài này, bạn sẽ áp dụng khái niệm ước và bội số để xem xem số a đã cho có chia hết cho số b hay không. Dựa vào kết quả đó để xác định liệu chúng có phải là ước hay bội của nhau hay không.
Xem thêm : Gateway là gì? Vai trò và ứng dụng gateway trong viễn thông
Bài 1: 48 có phải là bội – ước của 6 không?
- Phương pháp giải: Thực hiện phép chia 48 cho 6
- Vì 48 chia hết cho 6 => 48 là bội của 6 và 6 là ước của 48.
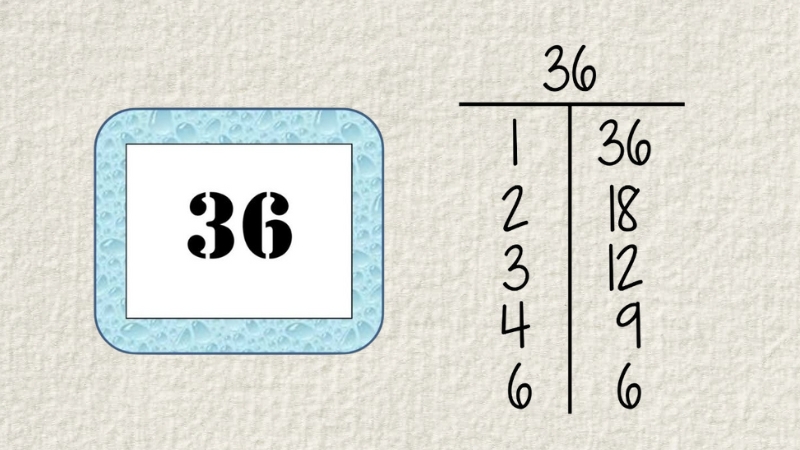
Bài 2: 36 có phải là bội của 12 hay không?
- Phương pháp giải: Thực hiện phép chia 36 cho 12
- Vì 36 chia hết cho 12 => 36 là bội của 12 => 36 thuộc tập hợp B(12)
Dạng 2: Xác định tập hợp ước, bội của một số
Để giải loại bài này, bạn chọn một số a bất kỳ và thực hiện phép chia lần lượt cho các số từ 1 đến a. Nếu a chia hết cho một số nào đó, thì số đó sẽ thuộc tập hợp ước của a. Để xác định bội của a, bạn nhân lần lượt a với các số tự nhiên từ 0 để có tập hợp bội của a.
Bài 1: Xác định tập hợp Ư(7).
Hướng dẫn giải:
Khi chia 7 cho các số từ 1 đến 7, ta thấy rằng 7 chỉ chia hết cho 1 và 7.
=> Kết luận: Ư(7) = {1; 7}
Bài 2: Tìm tập hợp các bội của 6 nhỏ hơn 40.
Hướng dẫn giải:
Bạn nhân 6 với các số tự nhiên 0; 1; 2; 3; 4; … để xác định tập hợp các bội của 6.
Được tập hợp các bội của 6: B(6) = {0; 6; 12; 18; 24; 30; 36; 42; 48; 54; 60;…}
Tuy nhiên, yêu cầu đề bài là tìm bội nhỏ hơn 40. Vậy nên: B(6) = {0; 6; 12; 18; 24; 30; 36}.
Dạng 3: Toán có lời văn
Để giải loại bài toán này, bạn cần đọc đề bài cẩn thận để xác định yêu cầu và chuyển nó thành bài toán tìm tập hợp bội số, ước số hoặc kiểm tra xem số đó có phải là bội, ước của số đã cho không. Sau đó, bạn sẽ áp dụng cách tìm bội số, ước số để hoàn thành bài toán.
Ví dụ: Hãy tính số học sinh của một trường biết rằng mỗi lần xếp hàng, hàng 6, hàng 7 đều đủ hàng và số lượng học sinh của trường dao động từ 415 đến 421 em.
Hướng dẫn giải:
Xem thêm : Khởi ngữ là gì? Tác dụng, dấu hiệu nhận biết và bài tập liên quan
Yêu cầu của đề bài là tìm số học sinh của trường. Gọi số học sinh đó là a. Trong đó: a ∈ N, 415 ≤ a ≤ 421.
- Xếp thành hàng 6, 7 đều đủ => a chia hết cho cả 6 và 7.
- Do đó: a ∈ B (6; 7) = {0; 42; 84; 126; …; 378; 420; 462; …}.
- Với 415 ≤ a ≤ 421 => a = 420
Vậy số học sinh của trường là 420 em.
Có Bao Nhiêu Ước của Số Nguyên Âm?
Trong lĩnh vực toán học, quy tắc tìm ước của một số cũng áp dụng cho các số nguyên âm.
Ví dụ: Xét số -12.
- Theo quy tắc, ước của -12 là {-12; -6; -4; -3; -2; -1; 1; 2; 3; 4; 6; 12}
- Mỗi số trong danh sách này có thể nhân với một số nguyên khác để được -12.
Trong các bài toán thực tế, nhất là ở cấp độ Toán 6, thường chỉ cần xác định ước và bội số tự nhiên khi đề bài không yêu cầu thêm.
Tập Hợp Các Ước Của 0 Là Gì?
Theo nguyên tắc xác định ước của một số, chúng ta biết rằng số 0 chia hết cho tất cả các số tự nhiên khác 0.
Do đó, tập hợp các ước của 0 bao gồm mọi số nguyên không phải là 0 (0 được coi là bội số của mọi số nguyên khác 0).
Giá trị của số 0 trong toán học?
Số 0 không phải là ước của bất kỳ số nào. Điều này xuất phát từ quy tắc rằng ước số của một số a phải lớn hơn 0.
Thêm vào đó, theo quy tắc của toán học, không tồn tại số nào có thể chia hết cho 0.
Trong ngữ cảnh chương trình Toán lớp 6, việc hiểu rõ về khái niệm ước và bội đóng vai trò quan trọng. Bài viết này sẽ giúp bạn tìm hiểu rõ hơn về ước và bội, cùng nhau khám phá các dạng toán liên quan.
Câu hỏi thường gặp
1. Ước và bội là khái niệm gì?
Ước và bội là khái niệm cơ bản trong toán học. Nếu một số a chia hết cho số b, ta gọi a là bội của b và ngược lại, b là ước của a.
2. Làm thế nào để tìm ước và bội của một số tự nhiên?
Để tìm ước của một số tự nhiên, chúng ta lần lượt chia số đó cho các số tự nhiên từ 1 đến chính số đó. Đối với việc tìm bội của một số, chúng ta nhân số đó với các số tự nhiên để thu được tập hợp bội của số đó.
3. Làm sao để nhận biết một số là ước hay bội của số khác?
Để nhận biết một số có phải là ước hay bội của số khác, chúng ta chỉ cần chia số đó cho số kia và xem kết quả để xác định tính chất của chúng.
Tóm tắt
Trong bài viết này, chúng ta đã tìm hiểu về khái niệm ước và bội, cách tìm ước và bội của một số tự nhiên cũng như các dạng bài tập liên quan. Để nắm vững kiến thức này, hãy áp dụng vào thực hành và không ngần ngại đặt câu hỏi khi cần clarification.
Đồng thời, hãy ghé thăm website để cập nhật thêm thông tin hữu ích và đừng quên chia sẻ bài viết nếu bạn thấy nó hữu ích. Chúc bạn thành công trong hành trình khám phá toán học!
Nguồn: https://laginhi.com
Danh mục: News



