Phương pháp đổi biến số trong Nguyên hàm và Tích phân

Việc tính toán nguyên hàm và tích phân thông qua phương pháp đổi biến số là một phần quan trọng và cực kỳ phổ biến trong chương trình toán học ở trình độ THPT. Những khái niệm về nguyên hàm và tích phân đang đốn tim nhiều học sinh. Vậy, bạn đã hiểu rõ về chúng chưa? Đừng lo lắng, Laginhi.com sẽ cùng bạn tìm hiểu về phương pháp đổi biến số để giải quyết bài toán về nguyên hàm và tích phân trong bài viết này!

Nguyên hàm: Khái niệm và cách tính

Khi xét hàm số f xác định trên tập K, ta định nghĩa hàm số F là nguyên hàm của f nếu đạo hàm của F(x) bằng f(x) với mọi x thuộc K.

Bạn đang xem: Phương pháp đổi biến số trong Nguyên hàm và Tích phân

Lưu ý: Đối với hàm số F là một nguyên hàm của f trên tập K, ta có thể biểu diễn một dạng tổng quát y=F(x)+C, trong đó C là một hằng số bất kỳ. Điều này ám chỉ rằng y=F(x)+C cũng là một nguyên hàm của f trên K.

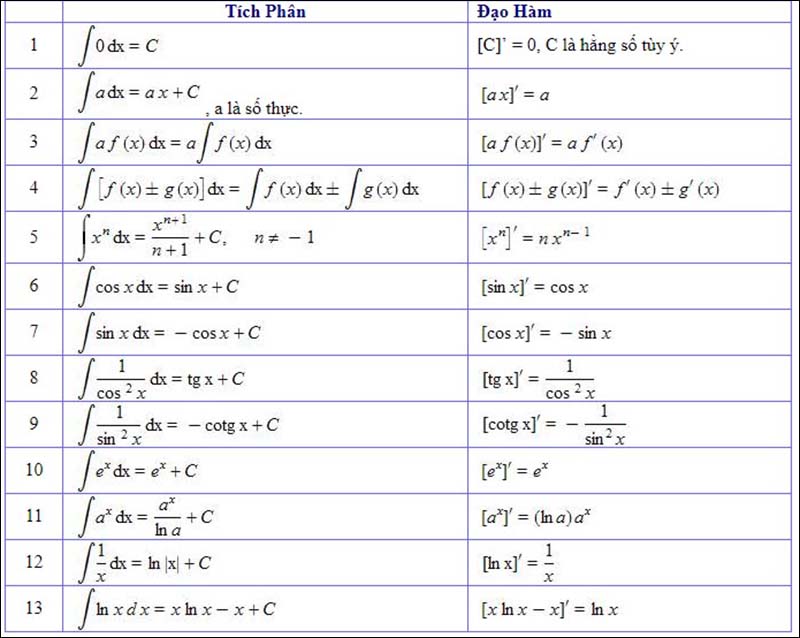
Một số công thức nguyên hàm cơ bản

Trong toán học, việc tính nguyên hàm là một phần quan trọng của việc giải các bài toán tích phân. Dưới đây là một số công thức tính nguyên hàm cơ bản mà bạn thường gặp:

• ∫0dx=C
• ∫dx=x+C
• ∫x^kdx=x^k+1/k+1+C với k≠1
• ∫1/xdx=ln|x|+C
• ∫a^xdx=a^x/lna+C với 0<a≠1

Ngoài ra, khi bạn gặp trường hợp với k là hằng số khác 0, các công thức sau sẽ hữu ích:

• ∫sinkxdx=−coskx/k+C
• ∫coskxdx=sinkx/k+C
• ∫e^kxdx=e^kx/k+C
• ∫1/cos2xdx=tanx+C
• ∫1/sin2xdx=−cotx+C

Ý Nghĩa của Tích Phân Trong Toán Học

Tích phân là một khái niệm toán học quan trọng, cùng với vi phân tạo thành cơ sở cho giải tích, là lĩnh vực năng động của số học. Trong đó, vi phân (differentiation) và tích phân hai đề tài không thể phân biệt.

Giả sử F(x) là nguyên hàm của hàm số f(x) trên đoạn (a, b). Tích phân không xác định (indefinite integral) được thể hiện thông qua công thức:

Phương pháp tính tích phân

Khi nghiên cứu về tích phân, có ba phương pháp cơ bản để tính toán bao gồm:

• Tính tích phân thông qua phương pháp phân tích.
• Tính tích phân bằng cách đổi biến.
• Tính tích phân theo từng phần cụ thể.

Một cách tiếp cận phổ biến là sử dụng bảng tích phân của một số hàm số sơ cấp dựa trên đạo hàm.

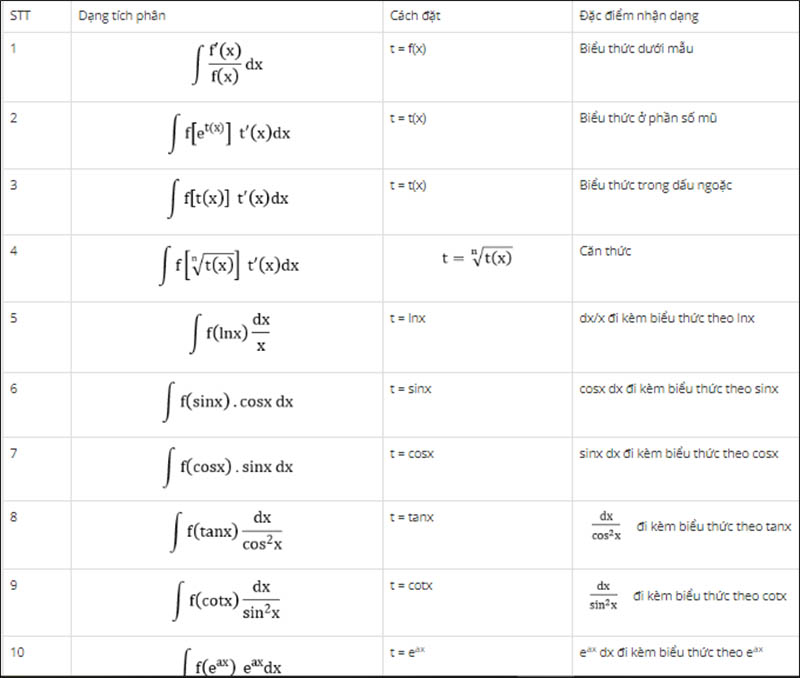
Giai Đoạn Biến Đổi Trong Nguyên Hàm

Một dạng phổ biến của bài toán là tìm nguyên hàm thông qua phương pháp biến đổi số. Cơ sở của phương pháp này trong việc tính toán nguyên hàm là chúng ta áp dụng định lý sau:

Cho hàm số u=u(x) có đạo hàm liên tục trên tập K và hàm số y=f(u) liên tục thỏa mãn f[u(x)] xác định trên tập K. Khi đó nếu F là một nguyên hàm của hàm số f thì: ∫f[u(x)]u′(x)dx=F[u(x)]+C

Phương pháp biến đổi số dạng 1

Để tính nguyên hàm của hàm số f(x), bạn cần thực hiện các bước sau:

Bước 1: Đặt t=u(x) với u(x) là một hàm số thích hợp. Khi đó dt=u′(x)dx

Bước 2: Thực hiện biến đổi ∫f(x)dx=∫g[u(x)].u′(x)dx=∫g(t)dt=G(t)+C

Bước 3: Thay t=u(x), từ đó bạn sẽ nhận được kết quả cuối cùng

Ví dụ minh họa:

Tìm ∫x^3/sqrt(2x^4+3)^3dx:

Cách giải:

Bước 1:

• x^3/sqrt(2x^4+3)^3dx=1/8.8x^3/sqrt(2x^4+3)^3dx=18.(2×4+3)′sqrt(2x^4+3)^3dx=18.d(2×4+3)/sqrt(2x^4+3)^3

Đặt t=2x^4+3. Khi đó:

• ∫x^3/sqrt(2x^4+3)^3dx=∫1/8.dt/sqrt(t)^3=∫(t^−1/3)/8dt=1/8.3/2.t^2/3+C=3sqrt(t^2)^3/16+C

Thay t=2×4+3 vào, bạn sẽ có:

• ∫x^3/sqrt(2x^4+3)^3dx=3sqrt(2x^4+3)^3/16+C

Phương Pháp Biến Đổi Dạng 2

Khi muốn tính nguyên hàm của hàm số f(x), bạn cần thực hiện các bước sau:

Bước 1: Đặt x=u(t) với u(t) là một hàm số phù hợp. Khi đó, dx=u′(t)dt

Bước 2: Thay đổi ∫f(x)dx=∫f[u(t)]u′(t)dt=∫g(t)dt=G(t)+C

Xem thêm : Thiện cảm là gì? Cách nói chuyện gây thiện cảm với người khác

Bước 3: Biến đổi G(t) theo x để thu được kết quả cuối cùng

Ví dụ:

Hãy tìm ∫dx/sqrt(1+x^2)^3

Cách giải:

Đặt x=tant với t∈[−π2;π2]

Do đó: dx=(tant)′dt=dtcos2t

Vậy chúng ta có:

∫dx/sqrt(1+x^2)^3=∫dt(1+tan2t)^3.cos^2t=∫costdt=sint+C

Vì x=tant nên:

x2=sin2tcos2t=sin2t1−sin2t

⇒x2(1−sin2t)=sin2t⇒sin2t(1+x2)=x2

⇒sint=x/sqrt(1+x^2)

Thay vào ta được: ∫dx(1+x2)3√=x1+x2√+C

Phương Pháp Đổi Biến Số Quy Về Tìm Nguyên Hàm

Kỹ thuật đổi biến số trong nguyên hàm là cách chúng ta sử dụng để tìm nguyên hàm của một hàm số. Sau đó, chúng ta thực hiện phép tính theo yêu cầu của bài toán.

Ví dụ:

Tìm ∫101−x2dx

Cách Giải:

Chúng ta giả sử x = sin t với t∈[−π2;π2]

Khi đó, dx=(sin t)′dt=cos t dt

Thay đổi ranh giới tích phân: Với x=0⇒t=0 và x=1⇒t=π2

Vậy:

∫1−x2dx = ∫1−sin2t cos t dt = ∫cos2t dt

= ∫cos2t + 1/2 dt = sin2t / 4 + t / 2

Do đó:

Xem thêm : Mưa là gì? Nguyên nhân, quá trình hình thành và các loại mưa

∫1 01−x2dx = sin2t / 4 + t / 2 ∣∣∣π2 0 = π / 4

Phương pháp chuyển đổi biến số đặc biệt

Trong một số bài toán tính tích phân I = ∫ba f(x)dx, bạn có thể sử dụng kỹ thuật đặt biến phụ: t = (a + b) – x và tận dụng tính chẵn lẻ của hàm số f(x) để giúp việc tính toán trở nên dễ dàng hơn.

Ví dụ:

Tính tích phân I = ∫1−1 x^2018 sinxdx

Cách giải:

Chúng ta có:

I = ∫1−1 x^2018 sinxdx = ∫0−1 x^2018 sinxdx + ∫1^0 x^2018 sinxdx(∗)

Đặt J = ∫0−1 x^2018 sinxdx

Đặt t = -x ⇒ dx = -dt

Chuyển đổi giới hạn: x = 0 ⇒ t = 0 và x = -1 ⇒ t = 1

Vì vậy, chúng ta có:

J = ∫0−1 x^2018 sinxdx = – ∫1^0 t^2018 sin(t)(-dt) = – ∫1^0 t^2018 sint dt

Thay vào (∗) ta có: I = 0

Xem thêm:

• Định nghĩa về số chính phương là gì? Dấu hiệu, Tính chất, Bài tập số chính phương
• Hàm số mũ là gì? Định nghĩa và Tính chất của hàm số mũ
• Số phức là gì? Modun số phức? Bài tập công thức số phức

Bài viết trên đây của một trang web đã giúp bạn hiểu rõ hơn về nguyên hàm, tích phân và phương pháp chuyển đổi biến số trong nguyên hàm và tích phân. Hy vọng kiến thức trong bài viết sẽ hỗ trợ bạn trong quá trình học tập và nghiên cứu về phương pháp chuyển đổi biến số. Chúc bạn thành công trong hành trình học tập của mình!

Tính tích phân, nguyên hàm bằng phương pháp đổi biến số là một khái niệm toán học quen thuộc nhưng vô cùng quan trọng trong chương trình toán học THPT. Hãy cùng tìm hiểu nguyên hàm là gì và phương pháp đổi biến số để tìm nguyên hàm, tích phân trong bài viết dưới đây.

Câu hỏi thường gặp

1. Nguyên hàm là gì?

   • Nguyên hàm của một hàm số f trên đoạn K là hàm số F sao cho đạo hàm của F tại mọi điểm x trong K bằng f(x).

2. Tích phân là gì?

   • Tích phân là một phép tính cơ bản trong toán học, đôi khi được coi là phép nghịch đảo của vi phân.

3. Phương pháp đổi biến số là gì?

   • Đây là một trong những phương pháp quan trọng để tìm nguyên hàm và tích phân của một hàm số, thông qua việc thực hiện biến đổi các biến số trong phép tính.

4. Cách tính nguyên hàm sơ cấp?

   • Có một số công thức nguyên hàm cơ bản thường được sử dụng, bao gồm tích phân của các hàm số như hàm số hằng, hàm số mũ, hàm số sin, cos, và e^x.

5. Lý thuyết của phương pháp đổi biến số?

   • Phương pháp này dựa trên việc sử dụng định lý về việc thay đổi biến số để giải các bài toán liên quan đến nguyên hàm và tích phân.

6. Các bước thực hiện phương pháp đổi biến số?

   • Bước 1: Đặt biến u=u(x) sao cho u′(x)dx thể hiện phép biến đổi.
   • Bước 2: Thực hiện các phép biến đổi để đưa về dạng tích phân dễ tính.
   • Bước 3: Thay đổi biến số và giải phương trình để tìm nguyên hàm cần tính.

7. Ví dụ minh họa về phương pháp đổi biến số?

   • Một ví dụ cụ thể là việc tính nguyên hàm của hàm số x^3/sqrt(2x^4+3)^3 bằng phương pháp đổi biến số.

Tóm tắt

Trên đây là những kiến thức căn bản về nguyên hàm, tích phân và phương pháp đổi biến số trong toán học. Để nắm vững hơn về chủ đề này, hãy thực hành và áp dụng những phương pháp này vào các bài toán cụ thể. Hãy liên hệ với trang web để tìm hiểu thêm và áp dụng kiến thức này vào thực tế.

Nguồn: https://laginhi.com
Danh mục: News