R là tập hợp số gì? Số thực R gồm số nào? Ví dụ

Khi bắt đầu hành trình khám phá về con số R, không ít người cảm thấy bối rối với khái niệm này trong toán học. Tuy nhiên, để nắm vững và hiểu rõ hơn về R, đó chính là lúc chúng ta cần kỹ thuật và kiến thức. Laginhi.com sẽ dẫn dắt bạn qua từng bước, từ các ví dụ đến những khái niệm căn bản về số thực, từ những tính chất quan trọng nhất đến vai trò to lớn của số thực trong lĩnh vực toán học. Hãy cùng đồng hành và khám phá điều thú vị đằng sau R, tập hợp số này nhé.

Số thực R là gì?

R là tập hợp số nào? R là tập hợp số thực gồm tất cả các số hữu tỉ như − 6 và phân số 8/3 cùng với tất cả các số vô tỉ như √2 = 1.41421356… và số 0.

Bạn đang xem: R là tập hợp số gì? Số thực R gồm số nào? Ví dụ

Để định nghĩa, R là tập hợp số thực bao gồm số dương như 1, 2, 3, 4, số 0, số âm như -1, -2, -3, -4, các số vô tỉ và hữu tỉ. R được ví như các điểm trên trục số dài vô hạn.

Số 0 cũng là số thực vì nó không phải là số nguyên âm hay dương. Số nguyên là một phần của R, vì vậy số 0 là một thành viên của tập hợp số thực.

Đặc điểm của tập số thực R

– Mọi số thực khác không đều là số âm hoặc dương.

– Tổng/tích của hai số thực không âm vẫn là số không âm.

– Số thực là một tập vô hạn, chúng ta không thể đếm được các số thực.

– Tồn tại một hệ thống các tập con vô hạn có thể đếm được của tập số thực R (R = Q U I)

Trong đó:

• N: Tập hợp các số tự nhiên
• Z: Tập hợp các số nguyên
• Q: Tập hợp số hữu tỉ
• I = RQ: Tập hợp các số vô tỉ

– Số thực được sử dụng để biểu thị các đại lượng liên tục.

– Số thực có thể được biểu diễn dưới dạng hệ thập phân.

Trục R tập hợp số thực

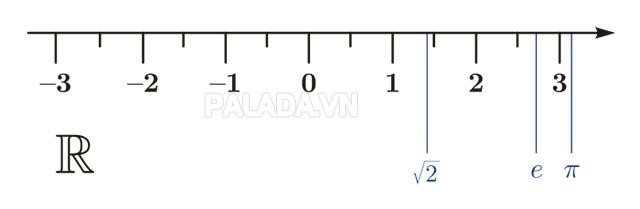
Mỗi số thực được biểu diễn bởi một điểm trên trục số và ngược lại, mỗi điểm trên trục số sẽ biểu diễn một số thực. Chỉ có tập hợp số thực R mới có thể lấp đầy trục số.

Trong R tập hợp số thực, ta cũng có các phép toán cộng trừ, nhân, chia, lũy thừa, căn bậc… Trong các phép toán với số thực cũng có các tính chất như phép toán trong tập hợp các số hữu tỉ.

Ta có: N ⊂ Z ⊂ Q ⊂ R.

Các đặc tính của tập số thực R

Xem thêm : Event là gì? Tìm hiểu tất tần tật về ngành nghề tổ chức sự kiện

Khi nhắc đến ký hiệu R trong môn toán, chúng ta đề cập đến tập hợp số thực và những đặc tính sau:

– Tập hợp R bao gồm tất cả các số thực, tạo thành một trường số với các phép toán cộng, nhân và chia cho các số khác không. Các số này có thể được sắp xếp trên một trục số theo cách phù hợp với phép cộng và phép nhân.

– Khi nói đến tập số thực R, nếu một tập con không rỗng của số thực có giới hạn trên, thì nó sẽ có giới hạn trên là một số thực nhỏ nhất.

Ứng Dụng Của Tập Hợp Số Thực R

Với những đặc điểm đã được nêu trên, tập hợp số thực R được áp dụng rộng rãi trong nhiều lĩnh vực khác nhau. Hãy cùng khám phá các ứng dụng thú vị của nó.

1. Trong Toán Học:

Tập hợp số thực R đóng vai trò quan trọng trong giải tích và hình học. Nó giúp mô hình hóa và giải quyết các vấn đề phức tạp trong không gian và thời gian.

2. Trong Kỹ Thuật:

Rất nhiều ứng dụng của số thực R có sự hiện diện trong các lĩnh vực kỹ thuật như công nghệ thông tin, điện tử, xây dựng cầu đường, vận tải, v.v. Sự chính xác của số thực rất quan trọng để đảm bảo tính an toàn và hiệu quả của các dự án kỹ thuật.

3. Trong Kinh Tế Học:

Việc ứng dụng số thực R trong phân tích tài chính, dự báo xu hướng thị trường và tính toán tài chính là không thể phủ nhận. Các thuật toán số học phức tạp dựa trên số thực giúp cho việc ra quyết định kinh doanh một cách chính xác và minh bạch.

4. Trong Công Nghệ Thông Tin:

Số thực R cũng được ứng dụng rộng rãi trong lĩnh vực công nghệ thông tin, đặc biệt là trong lĩnh vực xử lý tín hiệu, truyền thông và mã hóa thông tin. Không thể phân biệt rõ giữa việc sử dụng số thực và công nghệ thông tin trong thế giới kỹ thuật ngày nay.

Những ứng dụng của tập hợp số thực R trên chỉ là một phần nhỏ của những cơ hội mà nó mang lại. Hãy tiếp tục tìm hiểu và khám phá thêm về sức mạnh của số thực trong các lĩnh vực khác nhau.

Ưu điểm của Số thực R và logic

Hãy khám phá sự phong phú và sâu rộng của các số thực R liên quan đến logic và toán học trong bài viết này. Số thực R, mặc dù thường được chuẩn hóa theo tiên đề Zermelo-Fraenkel của lý thuyết tập hợp, nhưng thu hút sự quan tâm của nhiều nhà toán học với các cơ sở logic khác nhau trong toán học. Đặc biệt, các số thực R đang được khám phá và nghiên cứu một cách sâu sắc trong lĩnh vực toán học kiến thiết và toán học đảo ngược, mở ra những cánh cửa mới của tri thức toán học.

Khám phá Số thực R

Xem thêm : Cộng sinh là gì? Một số ví dụ về cộng sinh trong tự nhiên

Trong toán học, Số thực R đóng vai trò quan trọng trong việc mô phỏng thế giới thực và ứng dụng rộng rãi trong nhiều lĩnh vực khác nhau như vật lý, kinh tế học và máy tính học. Việc nghiên cứu và hiểu rõ về các tính chất và ứng dụng của Số thực R mang lại cái nhìn sáng suốt và đột phá trong giải quyết các vấn đề phức tạp.

Vai trò của logic trong nghiên cứu Số thực R

Logic đóng vai trò then chốt trong việc xác định tính chất và quy luật của Số thực R. Việc áp dụng logic vào nghiên cứu về Số thực R giúp làm sáng tỏ mối liên hệ giữa các yếu tố và dẫn đến những phát hiện mới mẻ trong lĩnh vực này.

Đóng góp của Số thực R vào toán học kiến thiết và đảo ngược

Sự hiểu biết về Số thực R không chỉ là căn cơ cho các lý thuyết toán học hiện đại mà còn mở ra những khía cạnh mới trong toán học kiến thiết và đảo ngược. Việc áp dụng và khám phá Số thực R trong các lĩnh vực này giúp tạo ra sự đổi mới và phát triển toàn diện của toán học.

Hãy đồng hành cùng chúng tôi khám phá thế giới rộng lớn của Số thực R và logic, nơi mà tri thức và sự sáng tạo gặp nhau để tạo nên những khám phá kỳ diệu và đột phá trong lĩnh vực toán học.

Ứng dụng R tập hợp số thực vật lý

Trong lĩnh vực khoa học vật lý, phần lớn các hằng số vật lý như vị trí, diện tích, khối lượng… có thể được biểu diễn thông qua số thực.

Trong lĩnh vực toán học, khái niệm về tập hợp số thực không còn quá xa lạ với chúng ta. Tuy nhiên, không phải ai cũng hiểu rõ về nó. Trong bài viết này, chúng ta sẽ cùng tìm hiểu về tập hợp số thực R là gì, bao gồm các ví dụ và những khái niệm cơ bản liên quan. Hãy cùng đào sâu để hiểu rõ hơn về vai trò quan trọng của số thực trong lĩnh vực toán học.

Câu hỏi thường gặp

1. Tập hợp số thực R là gì?

   • Tập hợp số thực R bao gồm tất cả các số hữu tỉ và vô tỉ, cũng như số 0.

2. Định nghĩa của số thực R như thế nào?

   • Số thực R là tổng hợp của số dương, số âm, số hữu tỉ và số vô tỉ trên một trục số vô hạn.

3. Tính chất nổi bật của tập số thực R là gì?

   • Các số thực trong R có thể là số âm hoặc số dương và tổng/tích của hai số không âm vẫn là số không âm.

4. Vai trò của tập hợp số thực R trong toán học?

   • Số thực R được sử dụng để thể hiện các đại lượng liên tục và có thể biểu diễn dưới dạng thập phân.

5. Trục số thực R có ý nghĩa như thế nào?

   • Trục số thực là nơi mà mỗi số thực được biểu diễn bằng một điểm trên trục số, cung cấp các phép toán cộng trừ, nhân, chia và các tính chất tương tự như tập hợp các số hữu tỉ.

Tóm tắt

Trên tinh thần tổng quan, tập hợp số thực R đóng vai trò quan trọng trong lĩnh vực toán học, bao gồm các số hữu tỉ, số vô tỉ và cả số 0. Việc hiểu rõ về tính chất và ứng dụng của số thực R không chỉ giúp chúng ta trong giải các bài toán mà còn mở ra nhiều cơ hội nghiên cứu và ứng dụng trong thực tế.

Nếu bạn muốn khám phá thêm về tập hợp số thực R và áp dụng kiến thức này vào thực tế, hãy tiếp tục đọc và nghiên cứu để nắm vững kiến thức. Hãy truy cập trang web của chúng tôi để cập nhật thông tin mới nhất và học hỏi thêm nhiều kiến thức bổ ích!

Nguồn: https://laginhi.com
Danh mục: News