2 tam giác đồng dạng là gì? Lý thuyết và dạng bài tập

Những bí ẩn xoay quanh “2 tam giác đồng dạng” sẽ được hé lộ trong bài viết này. Đã từ lâu, kiến thức về “2 tam giác đồng dạng” không còn xa lạ với chúng ta. Tận dụng cách chứng minh tam giác đồng dạng trong giảng dạy Toán lớp 9, LaGiNhi sẽ cung cấp cái nhìn toàn diện về chủ đề này, từ lý thuyết đến các bài tập minh họa. Sẵn sàng khám phá sự liên kết biết bao giữa những tam giác này chưa? Hãy cùng nhau tìm hiểu và vận dụng những kiến thức hữu ích này vào thực tế thông qua các ví dụ cụ thể mà LaGiNhi mang đến!

Tính Đồng Dạng của Hai Tam Giác

Khái niệm về tính đồng dạng của hai tam giác rất quan trọng trong học hình học. Hai tam giác được coi là đồng dạng khi chúng có các góc tương ứng bằng nhau và các cạnh tương ứng tỉ lệ với nhau.

Bạn đang xem: 2 tam giác đồng dạng là gì? Lý thuyết và dạng bài tập

Các Trường Hợp Đồng Dạng của Tam Giác:

• Hai tam giác có 3 cặp cạnh tương ứng tỉ lệ với nhau được gọi là tam giác đồng dạng theo trường hợp cạnh-cạnh-cạnh.

Ví dụ về trường hợp này là khi xét tam giác ABC và tam giác A’B’C’, ta thấy chúng đồng dạng với nhau theo nguyên tắc cạnh-cạnh-cạnh.

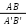
• Hai tam giác có 2 cặp góc tương ứng bằng nhau cũng được coi là đồng dạng, theo trường hợp góc-góc.

Một ví dụ điển hình là khi so sánh tam giác ABC và tam giác A’B’C’, ta thấy chúng đồng dạng với nhau dựa trên nguyên tắc góc-góc.

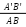
• Hai tam giác có 2 cặp cạnh tương ứng tỷ lệ + góc xen giữa 2 cặnh ấy bằng nhau cũng thuộc trường hợp tam giác đồng dạng, theo trường hợp cạnh-góc-cạnh.

Chẳng hạn, khi so sánh tam giác ABC và tam giác A’B’C’, ta thấy chúng đồng dạng với nhau theo nguyên tắc cạnh-góc-cạnh.

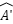
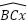
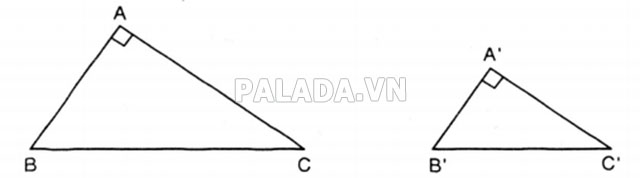
*Các Trường Hợp Đồng Dạng của Tam Giác Vuông

Định lí 1: Nếu cạnh huyền và cạnh góc vuông của một tam giác tỉ lệ với cạnh huyền và cạnh góc vuông của một tam giác khác, thì hai tam giác đó đồng dạng.

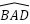
Ví dụ, với giả thiết tam giác ABC và tam giác A’B’C’, 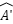= = 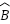90°; =

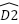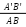
Kết luận: Tam giác ABC đồng dạng với tam giác A’B’C’.

Định lí 2: Nếu 2 cạnh góc vuông của một tam giác vuông tỉ lệ với 2 cạnh góc vuông của một tam giác vuông khác, thì hai tam giác đó đồng dạng.

Ví dụ, trong trường hợp tam giác ABC và tam giác A’B’C’, 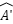= = 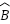90°; =

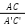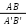
Kết luận: Tam giác ABC đồng dạng với tam giác A’B’C’.

Định lí 3: Nếu góc nhọn của một tam giác vuông bằng góc nhọn của một tam giác vuông khác, thì hai tam giác đó cũng đồng dạng.

Ví dụ, với giả thiết tam giác ABC và tam giác A’B’C’, 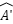= = 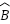90°

Kết luận: Tam giác ABC đồng dạng với tam giác A’B’C’.

Tính chất tam giác đồng dạng là gì?

Từ 2 tam giác đồng dạng, chúng ta suy ra được:

• Tỉ số 2 đường phân giác, đường cao, đường trung tuyến, bán kính nội tiếp và ngoại tiếp, chu vi tương ứng của hai tam giác đồng dạng đó bằng với tỉ số đồng dạng.
• Tỉ số diện tích của 2 tam giác đồng dạng = bình phương tỉ số đồng dạng.
  

  Chứng Minh 2 Tam Giác Đồng Dạng

  Chứng Minh Hai Tam Giác Đồng Dạng – Hệ Thức

Bài Toán: Cho tam giác ABC (AB<AC), AD là phân giác. Miền ngoài vẽ tia Cx cho 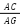= . Gọi I là giao điểm của Cx, AD. Chứng minh rằng:

1. a) Tam giác ADB ∼ tam giác CDI
2. b) AD.AC = AB.AI

c) AD² = AB.AC – BD.DC

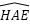
• Khi so sánh tam giác ADB và tam giác CDI, ta có 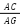= : (giả thiết)

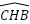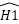⇾ = (đối đỉnh) => Tam giác ADB ~ tam giác CDI

1. b) Khi so sánh tam giác ABD và tam giác AIC, ta có: = 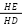(tam giác ADB ~ tam giác CDI); 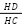= (AD là phân giác)

⇾ ∆ABD ~ ∆AIC => 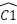= 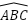⇾ AD.AI = AB.AC (1)

1. c) Có = ; (tam giác ADB ~ tam giác CDI) => AD.DI = BD.CD (2) từ (1) và (2): AB.AC – BD.CD = AD.AI – AD.DI = AD(AI – DI) = AD²

-Chứng minh hai tam giác đồng dạng – Định lí Talet + 2 đường thẳng song song

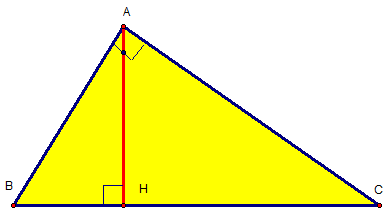
Bài toán: Cho ∆ABC nhọn, đường cao BD; CE. Kẻ 2 đường cao DF; EG của ∆ADE. Chứng minh:

1. a) △ADB∼△AEG
2. b) AD.AE = AB.AG = AC.AF
3. c) FG // BC

1. a) Xét ∆ABD và ∆AEG, ta có :

Xem thêm : Ăn ốc nói mò là gì? Ăn ốc nói mò là phương châm hội thoại nào?

BD⊥AC (BD là đường cao)

EG⊥AC (EG là đường cao)

Suy ra: BD // EG

Suy ra: △ADB∼△AEG

1. b) Từ a) Suy ra được ABAE=ADAG

⇒ AD.AE = AB.AG (1)

CM tương tự, ta được : AD.AE = AC.AF (2)

Từ (1) và (2) suy ra :

AD.AE = AB.AG = AC.AF

1. c) Xét tam giác ABC, ta có :

AB.AG = AC.AF (cmb) suy ra: =

Suy ra: FG // BC (Talet đảo)

-Chứng minh 2 tam giác đồng dạng – góc tương ứng bằng nhau

Bài toán: Cho △ABC có 2 đường cao BD + CE cắt nhau tại H. Chứng minh:

1. a) △HBE∼△HCE
2. b) △HED∼△HBC

và =

1. a) Xét △HBE và △HCD, ta có :

= =90∘ (gt)

= (đối đỉnh)

Suy ra: △HBE∼△HCD (g – g)

1. b) Xét △HED và △HBC, ta có :

=(△HBE∼△HCD)

Suy ra: =

= (đối đỉnh)

Suy ra △HED∼△HBC(c – g – c)

Suy ra: = (1)

Lại có: đường cao BD + CE cắt nhau tại H (gt)

Do đó, điểm H là trực tâm => AH⊥BC tại M.

Suy ra = =90∘

Mặt khác : = =90∘

Suy ra: = (2)

Từ (1) và (2) => =

hay: =

Tổng hợp các cách chứng minh 2 tam giác đồng dạng lớp 8

Hãy cùng tìm hiểu những phương pháp chứng minh 2 tam giác đồng dạng trong chương trình học lớp 8.

• Phương pháp 1: Hai tam giác đồng dạng khi chúng có các cặp cạnh tương ứng tỷ lệ + các góc tương ứng tỷ lệ.

• Phương pháp 2: Định lý Talet: Khi một đường thẳng song song với một cạnh của tam giác và cắt hai cạnh còn lại, chúng sẽ tạo ra trên cạnh đó những đoạn thẳng tương ứng tỉ lệ.

• Phương pháp 3: Kiểm tra các điều kiện cần và đủ để 2 tam giác đồng dạng: 2 tam giác có các cặp cạnh tương ứng tỷ lệ sẽ đồng dạng; 2 tam giác có 2 cặp góc tương ứng bằng nhau sẽ đồng dạng; 2 tam giác có 2 cặp cạnh tương ứng tỷ lệ, 2 góc xen giữa 2 cặp cạnh này bằng nhau sẽ đồng dạng.

• Phương pháp 4: Chứng minh bằng TH 1 (cạnh-cạnh-cạnh): Nếu ba cạnh của một tam giác tương ứng tỷ lệ với ba cạnh của tam giác khác, thì hai tam giác đó sẽ đồng dạng.

• Phương pháp 5: Chứng minh bằng TH 2 (cạnh-góc-cạnh): Nếu hai cạnh của một tam giác tương ứng tỷ lệ với hai cạnh của tam giác khác và hai góc tạo bởi hai cặp cạnh đó bằng nhau, thì hai tam giác sẽ đồng dạng.

Dạng 1: Phương pháp CM 2 tam giác đồng dạng – Sử dụng hệ thức:

Bài tập: Cho tam giác ABC có góc A vuông, đường cao AH. CM các hệ thức sau:

1. CMR AB2 = BH.BC và AC2 = CH.BC
2. CMR AB2 + AC2 = BC2
3. CMR AH2 = BH.CH
4. CMR AH.BC = AB.AC

Xem thêm : Starch là gì? Một số loại starch phổ biến và công dụng của chúng

a.Xét tam giác ∆ABC và ∆HAC, ta có:

Góc BAC = góc AHC = 90 độ

Góc C là góc chung

Vậy tam giác ∆ABC ~ ∆HAC (theo định lý g – g trong tam giác vuông)

Vậy AC/HC = BC/AC

AC2 = CH.BC (1)

CM tương tự ta có : AB2 = BH.BC (2)

1. Từ (1) và (2) vừa chứng minh ở trên, ta có :

AB2 + AC2 = BH.BC + CH.BC = (BH + CH)BC = BC2

1. Xét 2 tam giác ∆HBA và ∆HAC, ta có :

Góc BHC = góc AHC = 90 độ

Góc ABH = CAH (cùng phụ góc BAH)

Vậy kết luận ∆HBA ~ ∆HAC (tính chất g – g trong tam giác vuông)

HA/HC = HB/HA

Vậy: AH2 = BH.CH

1. Ta có ∆ABC ~ ∆HAC

HA/AB = AC/BC

Vậy: HA.BC = AB.AC

Dạng 2: Chứng minh hai tam giác đồng dạng – Định lí Talet + hai đường thẳng song song

Bài toán: Cho ∆ABC nhọn. Vẽ 2 đường cao là BD+CE. Lần lượt vẽ các đường cao DF+EG của ∆ADE. Yêu cầu:

1. a) Hãy CMR ∆ABD ~ ∆AEG.
2. b) Hãy CMR AD.AE = AB.AG = AC.AF
3. c) Hãy CMR FG // BC

a) Xét ∆ABD và ∆AEG, ta có :

Xem thêm : Ăn ốc nói mò là gì? Ăn ốc nói mò là phương châm hội thoại nào?

BD⊥AC (BD là đường cao)

EG⊥AC (EG là đường cao)

=> BD // EG

=> ∆ABD ~ ∆AGE

1. b) Ta có AB/AE = AD/AG

=> AD.AE = AB.AG (1)

Chứng minh tương tự : AD.AE = AC.AF (2)

Từ dữ kiện (1) và (2) suy ra : AD.AE = AB.AG = AC.AF

1. c) Xét ∆ABC, ta có :

AB.AG = AC.AF => FG // BC (theo định lí đảo talet)

FAQs
1. Tam giác đồng dạng là khái niệm gì?
– Tam giác đồng dạng xảy ra khi chúng có các góc tương ứng bằng nhau và các cạnh tương ứng tỉ lệ nhau.

2. Cách chứng minh tam giác đồng dạng như thế nào?

   • Chứng minh tam giác đồng dạng thông qua các phương pháp: cạnh-cạnh-cạnh, cạnh-góc-cạnh, điều kiện cần và đủ, định lí Talet.

3. Tính chất của tam giác đồng dạng là gì?

   • Từ hai tam giác đồng dạng, chúng ta suy ra được các tỉ số và diện tích tương ứng của hai tam giác đó.

4. Cách thực hiện chứng minh tam giác đồng dạng – Hệ thức?

   • Chứng minh thông qua các hệ thức và bước thực hiện cụ thể với ví dụ minh họa.

5. Phương pháp chứng minh tam giác đồng dạng – Định lí Talet và đường thẳng song song?

   • Quy trình chứng minh hai tam giác đồng dạng sử dụng định lí Talet và mối quan hệ với đường thẳng song song.

6. Phương pháp chứng minh tam giác đồng dạng – Góc tương ứng bằng nhau?

   • Cách chứng minh hai tam giác đồng dạng dựa trên nguyên lý các góc tương ứng bằng nhau.

Summary
Trong bài viết này, chúng ta đã tìm hiểu về khái niệm tam giác đồng dạng, cách chứng minh chúng, tính chất cơ bản và các phương pháp chứng minh tam giác đồng dạng. Qua việc thể hiện các ví dụ và bài tập minh họa, chắc chắn rằng bạn sẽ hiểu rõ hơn về 2 tam giác đồng dạng và áp dụng chúng trong thực tế. Đừng ngần ngại thực hành nhiều bài tập để nâng cao hiểu biết và tránh sai lầm khi áp dụng kiến thức. Hãy bắt đầu thử sức mình ngay hôm nay để trang bị kiến thức toán hữu ích!

Nguồn: https://laginhi.com
Danh mục: News