Bạn đã bao giờ nghe đến khái niệm “trung điểm” chưa? Đây không chỉ là một khái niệm đơn thuần trong toán học mà còn ẩn chứa những điều thú vị đằng sau. Trong bài viết này, chúng ta sẽ cùng nhau khám phá rõ hơn về trung điểm và cách chứng minh điều này qua những phương pháp độc đáo.
Trung Điểm: Sự Hiểu Biết Đầy Hứng Thú
Trong toán học, Trung Điểm hay còn gọi là Điểm Chính Giữa, là một điểm quan trọng nằm trên một đoạn thẳng và cách đều hai đầu của đoạn thẳng đó. Trung Điểm chia đoạn thẳng thành hai phần bằng nhau, đó chính là điểm tâm quan trọng xác định vị trí trung tâm của đoạn thẳng.
Bạn đang xem: Trung điểm là gì? Tính chất, cách chứng minh trung điểm đoạn thẳng
Ví dụ: Giả sử có đoạn thẳng AB, Trung Điểm M của đoạn thẳng AB là điểm nằm ở giữa A và B sao cho AM=MB. Điều này biểu thị rằng M không chỉ là Trung Điểm mà còn là Điểm Chính Giữa của đoạn thẳng AB.

Tính chất trung điểm của đoạn thẳng
Trong lĩnh vực toán học, trung điểm có những đặc điểm riêng biệt, là điểm luôn nằm ở vị trí giữa. Trên phương diện hình học, trung điểm mang theo những đặc tính sau:
- Nếu M là trung điểm của đoạn thẳng AB, thì MA = MB = AB/2.
- Mỗi đoạn thẳng có thể chứa nhiều điểm ở vị trí giữa, nhưng chỉ có một trung điểm duy nhất, nơi mà sự cân bằng hoàn hảo xuất hiện.
- Trung điểm nằm ở vị trí giữa và chia đều cả hai đầu mút của đoạn thẳng.

Cách vẽ trung điểm của đoạn thẳng
Có nhiều cách để xác định trung điểm của một đoạn thẳng, nhưng 3 phương pháp sau đây là phổ biến nhất:
Sử dụng công thức toán học
Một cách đơn giản để xác định trung điểm của đoạn thẳng là sử dụng công thức toán học. Bạn có thể tính tọa độ trung điểm bằng cách lấy trung bình của tọa độ hai đầu mút của đoạn thẳng. Ví dụ, nếu điểm A có tọa độ (x1, y1) và điểm B có tọa độ (x2, y2), tọa độ của trung điểm sẽ là ((x1 + x2) / 2, (y1 + y2) / 2).
Sử dụng dây cung đồng tâm
Một phương pháp khác để xác định trung điểm của đoạn thẳng là sử dụng dây cung đồng tâm. Bạn có thể vẽ một dây cung từ hai đầu mút của đoạn thẳng và nối với tâm của dây cung đó. Điểm gặp nhau giữa dây cung và tâm chính là trung điểm của đoạn thẳng.
Sử dụng thước kẻ
Cách cuối cùng để xác định trung điểm là sử dụng thước kẻ. Đặt thước kẻ và đặt hai đầu mút của đoạn thẳng tại hai đầu của thước. Điểm chính giữa giữa hai đầu mút sẽ là trung điểm của đoạn thẳng.
Sử dụng thước thẳng
Sử dụng thước thẳng theo các bước sau:
- Vẽ đoạn thẳng AB có chiều dài tương ứng với yêu cầu (ví dụ 9cm) bằng thước thẳng có vạch kẻ.
- Theo tính chất của trung điểm, với M là trung điểm nên: MA = MB = AB/2 = 4.5 cm. Trên đoạn thẳng AB, chọn điểm M sao cho AM = 4.5cm để đạt được trung điểm.

Có thể bạn quan tâm:
- 1 thước bằng bao nhiêu mét, cm, dm, mm, dam, hm, km, tấc, phân, li?
- 1 độ bằng bao nhiêu phút, giây, radian? Cách chuyển đổi đơn vị độ (góc)
- Cách chuyển đổi inch sang m một cách chính xác, nhanh chóng bằng công cụ
Ghi chú về việc sử dụng compa để xác định trung điểm M của đoạn thẳng AB
Kỹ thuật sử dụng compa để xác định trung điểm M của đoạn thẳng AB là một phương pháp đơn giản và hiệu quả, bao gồm các bước cụ thể sau:
- Dùng compa để vẽ một đường tròn tâm A. Với khoảng cách giữa compa, tiếp tục vẽ một đường tròn tâm B có cùng bán kính.
- Sau đó, dựng giao điểm C và D của hai đường tròn đã vẽ. Tiếp theo, nối C với D để tạo thành đường thẳng.
- Trong quá trình này, giao điểm M của đường thẳng CD và đoạn thẳng AB sẽ chính là trung điểm cần tìm – trung điểm M.
Quan trọng khi thực hiện quy trình vẽ bằng compa:
- Bán kính của hai đường tròn không cần phải bằng chính độ dài của đoạn thẳng, nhưng cần phải lớn hơn 1/2 độ dài của đoạn thẳng.
- Nếu muốn, bạn có thể vẽ cung tròn thay vì nguyên hình tròn, vẫn đảm bảo tính chính xác.
- Hai đường tròn hoặc hai cung tròn phải có cùng bán kính để đảm bảo tính đồng đẳng trong quá trình vẽ.

Xác định trung điểm bằng cách gấp giấy
Trong trường hợp bạn không có dụng cụ thước kẻ hay compa để vẽ trung điểm, bạn vẫn có thể áp dụng phương pháp gấp giấy thủ công. Dưới đây là các bước bạn có thể thực hiện:
- Vẽ đoạn thẳng AB lên tờ giấy.
- Gấp tờ giấy sao cho điểm B trên hình vẽ trùng với điểm A, hoặc ngược lại, điểm A trùng với điểm B.
- Khi đó, điểm giao trên nếp gấp sẽ chính là trung điểm M mà bạn định tìm.

Các Phương Pháp Chứng Minh Trung Điểm của Đoạn Thẳng
Để chứng minh rằng một điểm là trung điểm của một đoạn thẳng, bạn cần áp dụng các tính chất hình học liên quan đến trung điểm. Dưới đây là một số phương pháp cơ bản để chứng minh trung điểm:
- Phương Pháp 1: Sử dụng tính chất của trung điểm: Nếu một điểm chia đoạn thẳng thành hai phần bằng nhau, thì điểm đó là trung điểm của đoạn thẳng.
- Phương Pháp 2: Sử dụng định lý Pythagore: Trên tam giác vuông, điểm chính giữa của cạnh huyền là trung điểm của đoạn thẳng nối hai đỉnh vuông của tam giác.
- Phương Pháp 3: Sử dụng hệ thức tọa độ: Nếu tọa độ của điểm trung điểm bằng trung bình cộng tọa độ của hai đầu mút của đoạn thẳng, thì điểm đó là trung điểm.
Cách Chứng Minh Trung Điểm Bằng Hình Vẽ
Khi chứng minh trung điểm của một đoạn thẳng bằng hình vẽ, bạn có thể sử dụng các bước sau:
- Đặt đoạn thẳng và đánh dấu hai đầu mút của đoạn thẳng.
- Vẽ một đường thẳng đi qua một điểm mà bạn nghi ngờ là trung điểm và song song với đoạn thẳng ban đầu.
- Chứng minh rằng hai tam giác tạo thành bởi các đoạn thẳng đó đồng dạng với nhau để chứng minh điểm đó là trung điểm.
Với các phương pháp và cách chứng minh trên, bạn có thể dễ dàng xác định và chứng minh trung điểm của một đoạn thẳng một cách chính xác và hiệu quả.
Chứng Minh Theo Tính Chất Trung Điểm (Cách Chứng Minh của Lớp 6)
Khi muốn chứng minh điểm M là trung điểm của đoạn thẳng AB, bạn cần xác định rằng M nằm ở giữa A, B và MA + MB.
Ví Dụ:
Giả sử đoạn thẳng AB=8cm với M là trung điểm AB. Trên AB, hãy chọn hai điểm là C, D sao cho AC = BD= 3cm. Bây giờ, hãy chứng minh rằng M chính là trung điểm của CD.
Cách Giải:
- Vì M là trung điểm của AB, nên MA = MB = 4cm.
- Vì M, C cùng phía với A và AM > AC, suy ra C nằm ở giữa AM.
- Do đó, MC = MA − CA = 1cm.
- Tương tự, MD = 1cm.
- Tính được: CD= AB − AC − BD =2cm.
Xem thêm : Quần thể là gì? Đặc trưng cơ bản, ví dụ của quần thể sinh vật
Như vậy, ta có: MC = MD = 1cm; MC + MD = CD ⇒ M chính là trung điểm của CD.

Chứng Minh Trung Điểm Tam Giác (Cách chứng minh trung điểm lớp 7)
Để chứng minh theo cách này, trước hết, bạn cần hiểu rõ các tính chất liên quan đến trung điểm trong tam giác.
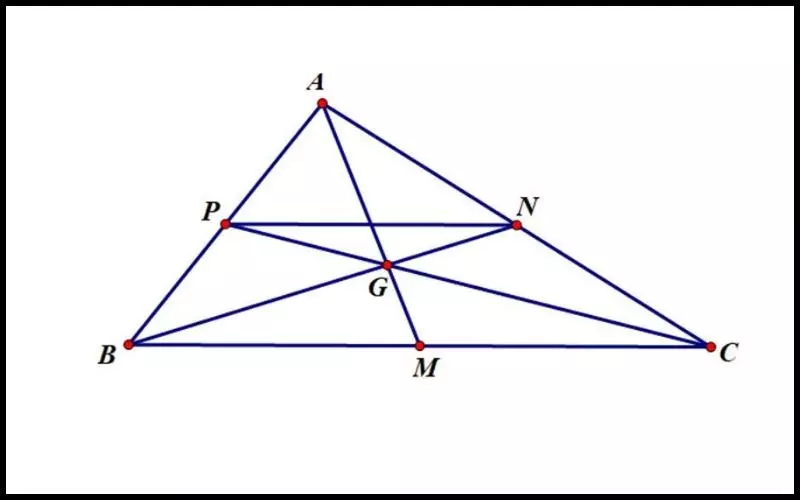
Cho tam giác ABC với M, N, P lần lượt là trung điểm của BC, CA, AB.
Khi đó:
- AM, BN, CP lần lượt được gọi là các đường trung tuyến của cạnh BC, CA, AB. Ba đường trung tuyến đồng quy tại điểm G được gọi là trọng tâm của tam giác ABC. Ba đoạn thẳng MN, NP, PM được gọi là các đường trung bình của tam giác ABC.
- Tính chất trọng tâm: Nếu G là trọng tâm tam giác ABC, thì AG, BG, CG lần lượt đi qua trung điểm của BC, CA, AB. Đồng thời: AG/AM = BG/BN = CG/CP = 2/3.
- Tính chất đường trung bình: Nếu MN là đường trung bình của tam giác ABC, thì MN song song và bằng 1/2 cạnh đáy tương ứng.
Ví dụ:
Cho tam giác ABC có AB > BC. BE là phân giác và BD là trung tuyến. Đường thẳng qua C vuông góc với BE cắt BE, BD, BA lần lượt tại F, G, K. DF cắt BC tại M. Chứng minh rằng: M là trung điểm đoạn BC.
Cách giải:
- Xét ΔBCK có:
BF vừa là đường cao, vừa là phân giác nên ΔBCK cân tại B
⇒ BC = BK và BF là trung tuyến
⇒ CF = FK.
- Xét ΔCKA có:
CF = FK; CD = DA ⇒ FD là đường trung bình
⇒ FD//AB ⇔ MD//AB
Mà CD = DA nên ⇒ CM/CB = CD/CA = 1/2
⇒ M là trung điểm BC.

Dựa vào tính chất tứ giác đặc biệt (Cách chứng minh trung điểm lớp 8)
Trong phần này, chúng ta sẽ tìm hiểu về một số tính chất đặc biệt của các tứ giác như sau.
Đường trung bình hình thang
Trong trường hợp hình thang ABCD với hai đáy là AB và CD, ta có điều kiện MN là đường trung bình của hình thang ABCD nếu MN song song với AB, có độ dài MN bằng một nửa tổng độ dài AB và CD, và M, N lần lượt là trung điểm của AB và BC.

Đường chéo hình bình hành
Trong hình bình hành ABCD với hai đường chéo AC và BD, ta biết rằng AC cắt BD tại trung điểm của mỗi đoạn.
Chú ý: Hình vuông, hình chữ nhật và hình thoi là những trường hợp đặc biệt của hình bình hành nên cũng sẽ có các tính chất được nêu trên.

Xem thêm : 1dm2 bằng bao nhiêu cm2, m2, km2 và cách đổi 1 dm2 ra m2
Ví dụ: Giả sử ABCD là hình bình hành với I là giao điểm của AC và BD. Chọn M bất kì trên CD. Đường thẳng MI cắt AB tại N. Cần chứng minh rằng I là trung điểm của MN.
Cách giải:
Vì ABCD là hình bình hành và I là giao điểm của hai đường chéo, ta có: DI = MI
Xét ΔDIM và ΔBIN:
- Góc DIM = góc BIN (hai góc đối nhau)
- DI = BI (đã chứng minh)
- Góc MDI = góc NBI (hai góc tương đương)
⇒ ΔDIM = ΔBIN (góc – cạnh – góc)
Vậy ⇒ IN = IM hoặc I chính là trung điểm của MN.
Dựa vào các tính chất của đường tròn (Cách chứng minh trung điểm lớp 9)
Trong phần này, chúng ta sẽ tập trung vào quan hệ giữa đường kính và dây cung trong đường tròn. Để hiểu rõ hơn, hãy xem xét đường tròn có tâm O và đường kính AB. MN là một dây cung bất kì của đường tròn. Nếu AB vuông góc với MN, thì AB sẽ đi qua trung điểm của MN, và ngược lại, nếu AB đi qua trung điểm của MN thì AB sẽ vuông góc với MN.

Ví dụ: Giả sử ta có tam giác ABC nhọn (AB < AC) nội tiếp đường tròn (O). Tiếp tuyến tại A và B của (O) cắt nhau tại M. Kẻ cát tuyến MPQ của (O) (với P nằm giữa M và Q) sao cho nó song song với BC và cắt AC tại E. Chúng ta cần chứng minh rằng E chính là trung điểm của đoạn thẳng PQ.
Cách giải:
Vì MA, MB là tiếp tuyến từ M đến đường tròn (O) nên ta có MA = MB.
Chúng ta có thể xác định ΔMAO và ΔMBO:
- MA = MB (đã chứng minh ở trên)
- MO là cạnh chung
- OA = OB (OA và OB là bán kính của đường tròn (O))
Do đó, ta suy ra ΔMAO = ΔMBO (theo nguyên lý cạnh – cạnh – cạnh).
Từ đó, có thể kết luận rằng: góc MOA = góc MOB ⇒ góc MOA = góc AOB/2 (1).
Do PQ∥BC ⇒ góc MEA = góc BCA (đồng vị), và vì góc BCA = góc AOB/2 ⇒ góc MEA = góc AOB/2 (2).
Từ (1) và (2) ta có: góc MEA = góc MOA.
Do đó, tứ giác MOEA là tứ giác nội tiếp.
Vì góc MEO = góc MAO = 90∘ (do MA là tiếp tuyến), ta suy ra rằng EO vuông góc với dây cung PQ ⇒ E chính là trung điểm của đoạn thẳng PQ.

Chứng minh trung điểm dựa vào tính chất đối xứng
- Đối xứng trục: Hai điểm A,B đối xứng với nhau qua đường thẳng d nếu d là đường trung trực của AB. Khi đó AB ⊥ d và d đi qua trung điểm của AB.
- Đối xứng tâm: Hai điểm A,B đối xứng với nhau qua điểm O nếu như O là trung điểm của AB.

### Câu hỏi thường gặp
-
Trung điểm là khái niệm gì?
Trung điểm là điểm nằm trên đoạn thẳng và cách đều hai đầu đoạn thẳng, chia đoạn thẳng thành 2 phần bằng nhau. -
Ví dụ minh họa về trung điểm?
Ví dụ: Trong đoạn thẳng AB, trung điểm M là điểm nằm giữa A, B và cách đều 2 điểm A, B hay MA=MB. -
Tính chất của trung điểm?
Trung điểm có tính chất: Nếu M là trung điểm của AB thì MA = MB = AB/2 và nằm giữa và cách đều 2 đầu mút của đoạn thẳng. -
Cách vẽ trung điểm của đoạn thẳng?
Có thể vẽ trung điểm bằng thước thẳng, compa hoặc gấp giấy theo các bước chi tiết cụ thể. -
Làm thế nào để chứng minh một điểm là trung điểm của một đoạn thẳng?
Để chứng minh một điểm là trung điểm của một đoạn thẳng, ta cần sử dụng các tính chất hình học và có thể áp dụng các phương pháp chứng minh khác nhau. -
Làm thế nào để xác định tọa độ trung điểm của đoạn thẳng trên mặt phẳng?
Để xác định tọa độ trung điểm của đoạn thẳng trên mặt phẳng, ta sử dụng công thức đơn giản với tọa độ của 2 điểm mút đoạn thẳng. -
Có bao nhiêu cách chứng minh trung điểm của đoạn thẳng?
Có nhiều cách chứng minh trung điểm, bao gồm chứng minh theo tính chất trung điểm, tính chất của tam giác, tứ giác đặc biệt, các tính chất của đường tròn và đối xứng. -
Tại sao trung điểm quan trọng trong hình học?
Trung điểm có vai trò quan trọng trong việc chia đoạn thẳng thành các phần bằng nhau và áp dụng trong nhiều bài toán hình học phức tạp khác. -
Cách xác định trung điểm bằng một phụ kiện nào đó?
Chúng ta có thể xác định trung điểm bằng cách sử dụng các công cụ như thước thẳng, compa hoặc phương pháp gấp giấy. -
Trung điểm của đoạn thẳng có ích gì trong thực tế?
Việc xác định trung điểm của đoạn thẳng giúp chia đoạn thẳng thành các phần bằng nhau, áp dụng trong thiết kế, định vị và nhiều lĩnh vực khác. -
Làm thế nào để hiểu rõ hơn về trung điểm trong hình học?
Để hiểu rõ hơn về trung điểm trong hình học, bạn có thể thực hành và áp dụng các phương pháp chứng minh và tính chất vào các bài tập cụ thể. -
Có cách nào khác để chứng minh trung điểm ngoài các phương pháp đề cập không?
Bên cạnh các phương pháp chứng minh trung điểm nêu trên, còn có thể áp dụng các phương pháp khác tùy theo yêu cầu và đặc điểm cụ thể của bài toán.
Nguồn: https://laginhi.com
Danh mục: News
