Chu vi là một khái niệm quan trọng không chỉ trong toán học mà còn trong hình học. Nó giúp chúng ta tính toán và đo lường các thuộc tính và kích thước của các hình học. Bạn đã bao giờ tự hỏi chu vi ký hiệu là gì chưa? Và công thức tính chu vi hình học được áp dụng ra sao chưa? Đừng bỏ lỡ cơ hội tìm hiểu về vấn đề này cùng với chúng tôi từ LagiNhi.com ngay trong bài viết dưới đây!
Chu vi ký hiệu là gì?
Chu vi đo khoảng cách từ điểm bắt đầu đến điểm kết thúc của hình. Đối với hình đa giác, chu vi tính bằng tổng độ dài các cạnh. Đối với hình không có cạnh, chu vi được tính bằng công thức hoặc đo đường bao quanh diện tích hình.
Bạn đang xem: Chu vi ký hiệu là gì? Công thức tính chu vi hình học
Với đa giác và các hình phẳng phổ biến, chu vi thường được ký hiệu là “c”. Đối với hình tròn, chu vi thường được ký hiệu là “C”.

Chu vi và cách tính chu vi hình tròn
Chu vi hình tròn hoặc chuỗi đường tròn là đường ranh giới ngoại cùng của hình tròn. Để tính chu vi hình tròn, bạn có thể nhân đường kính (d) với số pi hoặc nhân hai lần bán kính (r) với số pi.
Công thức: C = d.π hoặc C = 2.r.π
Trong công thức trên:
- C là đại lượng chu vi của hình tròn.
- d là chiều dài đường kính của hình tròn.
- r là chiều dài bán kính của hình tròn.
- Số pi có giá trị gần bằng 3,14 và được định nghĩa là tỷ lệ của chu vi hình tròn.
Ví dụ: Hãy tính chu vi của một cái bánh xe có bán kính 1,5m.
Giải:
Áp dụng công thức chu vi hình tròn, ta có:
C = 2.r.π = 2.1,5.3,14 = 9,42(m)

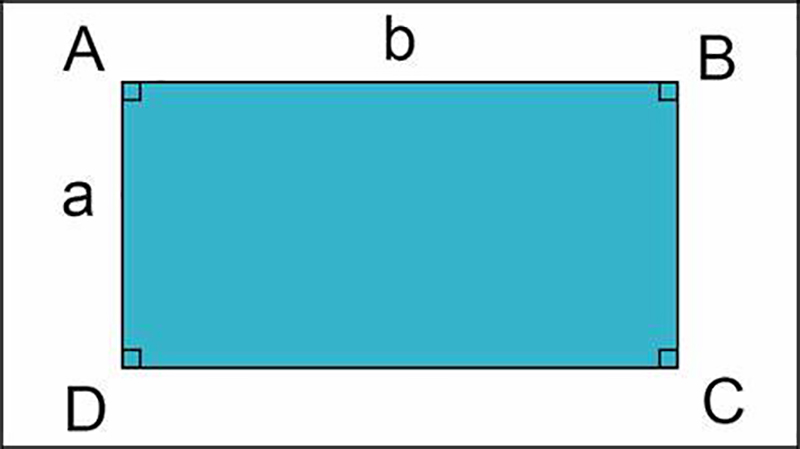
Chu vi và cách tính chu vi hình chữ nhật
Theo định nghĩa về chu vi, bạn có thể dễ dàng biết cách tính chu vi của hình chữ nhật sẽ bằng tổng bốn cạnh hoặc chiều dài cộng chiều rộng nhân 2.
Công thức: C = 2(a+b)
Trong đó:
- C là chu vi của hình chữ nhật.
- a là chiều dài.
- b là chiều rộng.
Ví dụ: Hãy tính chu vi của chiếc bánh hình chữ nhật khi biết chiều dài là 5cm và chiều rộng là 2cm.
Áp dụng công thức, chu vi của chiếc bánh hình chữ nhật là:
C = 2(a+b) = 2(5+2) = 14(cm)
Chu vi và cách tính chu vi hình vuông:
Xem thêm : F&B là gì? Nguồn gốc, vai trò và các bộ phận thuộc dịch vụ F&B
Tương tự như hình chữ nhật, hình vuông có 4 cạnh bằng nhau và 4 góc bằng 90 độ. Do đó, chu vi của hình vuông được tính bằng tổng 4 cạnh hoặc cạnh nhân 4.
Công thức: C = 4.a
Trong đó:
- C là chu vi của hình vuông.
- a là độ dài một cạnh của hình vuông.
Ví dụ: Nếu độ dài cạnh của một bảng hình vuông là 6cm, hãy tính chu vi của bảng đó.
Sử dụng công thức, chu vi của bảng hình vuông là:
C = 4.a = 6.4 = 24(cm)
Chu vi và cách tính chu vi hình tam giác
Theo quy tắc tính chu vi, chu vi của hình tam giác sẽ là tổng của 3 cạnh, bất kể loại tam giác nào như tam giác thường, tam giác vuông, tam giác đều, tam giác cân, tam giác tù, tam giác nhọn và tam giác vuông cân.
Công thức chung: C = a+b+c
Trong đó: a, b, c lần lượt là 3 cạnh của tam giác.
Đối với các loại tam giác đặc biệt, công thức có thể biến đổi như sau:
- Tam giác vuông (có một góc vuông): C = a+b+h (với h là chiều cao của tam giác, nối từ đỉnh xuống đáy).
- Tam giác đều (có ba cạnh bằng nhau): C = a.3
- Tam giác cân (có hai cạnh bằng nhau): C = 2.a+c hoặc C = 2b+c
Ví dụ: Cho một viên gạch hình tam giác:
- Có ba cạnh lần lượt là: 2cm, 3cm, 4cm
- Có ba cạnh bằng nhau và bằng: 3cm
- Có 2 cạnh bằng nhau lần lượt là: 2cm và còn lại 5cm
Giải:
Áp dụng công thức chu vi hình tam giác, ta có chu vi của viên gạch tam giác là:
C = a+b+c = 2+3+4 = 9(cm)
Vì viên gạch tam giác có 3 cạnh bằng nhau, nên đây là tam giác đều, do đó chu vi của viên gạch tam giác đều là:
C = a.3 = 3.3 = 9(cm)
Với viên gạch có hai cạnh bằng nhau, tam giác này là tam giác cân, ta có chu vi của viên gạch tam giác cân là:
C = 2.a+c = 2.2+5 = 9(cm)

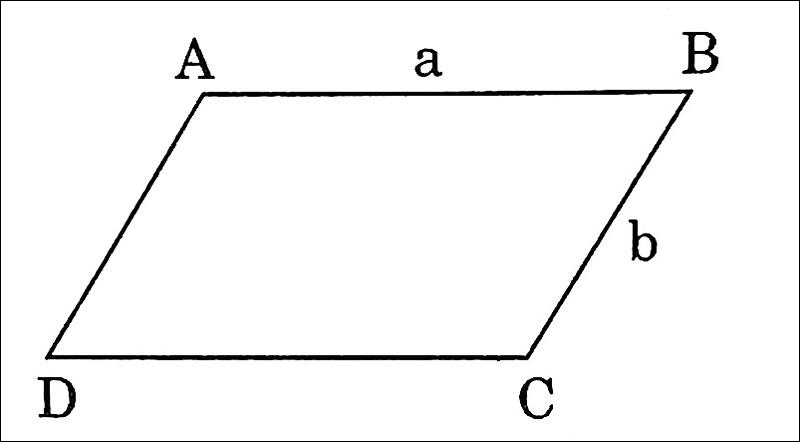
Chu vi và việc tính toán chu vi của hình bình hành
Xem thêm : Con lăn ghế massage là gì? Công dụng và cấu tạo của con lăn
Hình bình hành là một hình tứ giác có hai cặp cạnh đối song song và bằng nhau. Do đó, theo quy tắc tính chu vi, chu vi của hình bình hành sẽ bằng tổng độ dài của tất cả các cạnh.
Công thức: C = 2(a+b)
Trong đó:
- C là chu vi của hình bình hành.
- a và b: Là độ dài của hai cạnh liền kề bất kì của hình bình hành.
Ví dụ: Tính chu vi của một chiếc bánh hình bình hành khi biết độ dài các cạnh a = 4cm, b = 8cm.
Giải
Áp dụng công thức tính chu vi của hình bình hành, chu vi của chiếc bánh hình bình hành sẽ là:
C = 2(a+b) = 2(4+8) = 24(cm).
Chu vi là một khái niệm quan trọng trong toán học và hình học, được sử dụng để đo và tính toán các thuộc tính và kích thước của các hình học. Trong bài viết này, chúng ta sẽ cùng tìm hiểu các câu hỏi thường gặp liên quan đến chu vi và cách tính toán nó.
FAQs
-
Chu vi là gì?
- Chu vi là khoảng cách từ điểm bắt đầu đến điểm kết thúc của một hình.
-
Chu vi được ký hiệu như thế nào?
- Với đa giác và các hình phẳng thông thường, chu vi được kí hiệu là chữ “c”.
-
Cách tính chu vi hình tròn ra sao?
- Chu vi hình tròn bằng đường kính nhân với số pi hoặc bằng hai lần bán kính nhân với số pi.
-
Làm thế nào để tính chu vi hình chữ nhật?
- Chu vi của hình chữ nhật bằng tổng chiều dài và chiều rộng nhân 2.
-
Chu vi hình vuông được tính như thế nào?
- Chu vi hình vuông là tổng 4 cạnh hoặc một cạnh nhân 4.
-
Chu vi của hình tam giác tính như thế nào?
- Chu vi của hình tam giác bằng tổng 3 cạnh hoặc công thức cụ thể tùy vào loại tam giác.
-
Cách tính chu vi hình bình hành là gì?
- Chu vi hình bình hành bằng tổng độ dài các cạnh song song của hình.
-
Hình thang có cách tính chu vi ra sao?
- Chu vi hình thang là tổng 4 cạnh của hình thang đó.
Tóm Tắt
Trên đây là những thông tin cơ bản về chu vi trong hình học, bao gồm cách định nghĩa và cách tính toán chu vi của các hình học phổ biến như hình tròn, hình chữ nhật, hình vuông, hình tam giác, hình bình hành và hình thang. Để hiểu rõ hơn và áp dụng linh hoạt trong thực tế, hãy thực hành và ứng dụng những kiến thức này. Nếu cần hỗ trợ hoặc có thêm câu hỏi, đừng ngần ngại để lại bình luận dưới bài viết. Chúc bạn thành công trong việc học tập!
Nguồn: https://laginhi.com
Danh mục: News
