Là Gì Nhỉ (LaGiNhi) đang tạo ra sự chú ý với chủ đề “Hình chóp tam giác đều là gì?” Đây là một khái niệm trong hình học không gian mà chúng ta thường gặp từ thời cấp 2. Bài viết này sẽ cung cấp thông tin tổng quan về đặc điểm, tính chất, cách tính chu vi, diện tích và thể tích của hình chóp đều, kèm theo những dạng bài tập liên quan. Nếu bạn cần cập nhật kiến thức hoặc muốn làm mới lại khái niệm về hình chóp tam giác đều, hãy tham khảo ngay!
Định nghĩa hình chóp
Hình chóp là một khái niệm trong hình học không gian, được xác định bởi một mặt đáy là một đa giác lồi và các mặt bên là các tam giác có chung một đỉnh duy nhất được gọi là đỉnh của hình chóp. Có nhiều loại hình chóp khác nhau, với tên gọi dựa theo hình dạng của mặt đáy. Ví dụ, hình chóp tam giác có mặt đáy là hình tam giác, hình chóp tứ giác có mặt đáy là hình tứ giác. Trong trường hợp mặt đáy của hình chóp là các hình đặc biệt như tam giác đều hoặc tứ giác đều, thì đó được gọi là hình chóp đều.
Bạn đang xem: Hình chóp tam giác đều là gì? Tính chất, cách tính thể tích
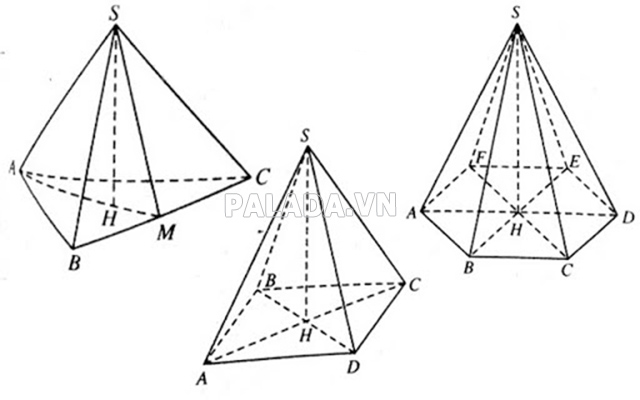
Tính chất hình chóp
- Đường cao của hình chóp là đường thẳng đi qua 1 đỉnh và vuông góc với mặt phẳng đáy của hình chóp đó.
- Tên gọi của hình chóp dựa vào hình dạng mặt đáy của hình chóp đó.
- Nếu hình chóp có cạnh bên tạo với mặt đáy các góc bằng nhau hoặc các cạnh bằng nhau, thì chân đường cao vừa là tâm đường tròn ngoại tiếp đáy.
- Nếu hình chóp có các mặt bên tạo với mặt đáy góc bằng nhau hoặc có các đường cao của mặt bên xuất phát từ 1 đỉnh bằng nhau, thì chân đường cao cũng chính là tâm đường tròn nội tiếp mặt đáy.
- Nếu hình chóp có mặt bên hoặc mặt chéo bất kỳ vuông góc với mặt đáy, thì đường cao của hình chóp đồng thời cũng là đường cao của mặt bên hoặc mặt chéo đó.
Định nghĩa hình chóp tam giác đều
Hình chóp tam giác đều là dạng hình chóp mà mặt đáy được hình thành từ tam giác đều, với các mặt bên cũng tạo nên các tam giác cân có chung một đỉnh.
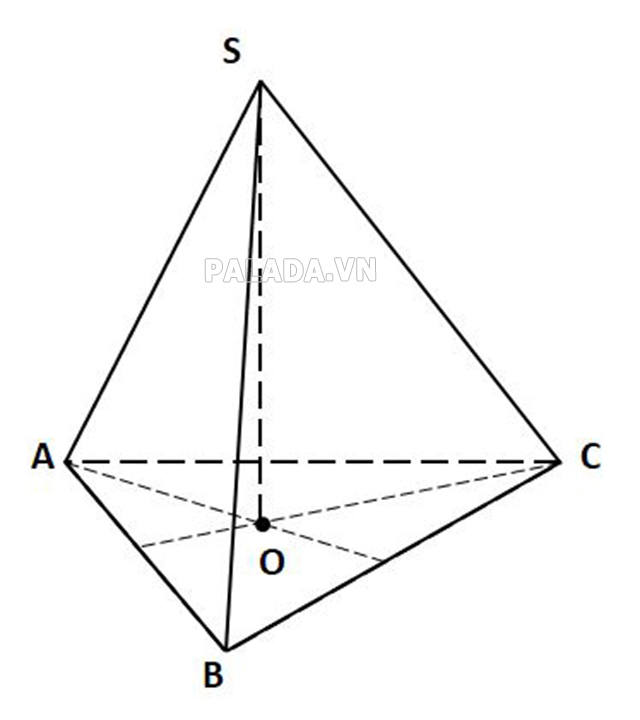
Hình chóp tam giác đều
Đặc điểm của hình chóp tam giác đều bao gồm:
- Có 3 mặt phẳng đối xứng
- Mặt đáy là tam giác đều
- Các cạnh bên đều bằng nhau
- Các mặt bên là hình tam giác cân và bằng nhau
- Chân đường cao trùng với tâm mặt đáy
- Góc tạo bởi các mặt bên và mặt đáy bằng nhau
- Góc tạo bởi cạnh bên và mặt đáy bằng nhau
Tâm của tam giác đều đồng thời là giao điểm của 3 đường trung tuyến, đường cao, đường trung trực và đường phân giác trong.
Cách Tính Chu Vi của Hình Chóp Tam Giác Đều
Để tính chu vi của một hình chóp, bạn cần cộng tổng chu vi của mặt đáy với chu vi của các mặt bên.
Công thức:
P = Pđáy + Pcác mặt bên
Trong đó:
- Pđáy là chu vi của mặt đáy
- Pcác mặt bên là tổng chu vi của các mặt bên
Xem thêm : Cô đơn là gì? Sự khác nhau giữa cô đơn và cô độc?
Phương pháp tính diện tích hình chóp tam giác đều
Diện tích hình chóp tam giác đều bao gồm diện tích xung quanh và diện tích toàn phần.
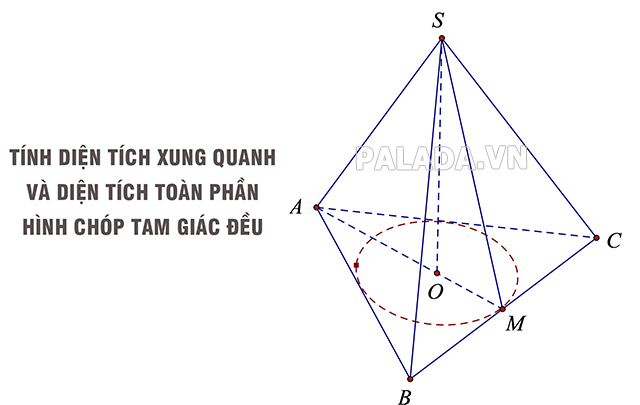
- Diện tích xung quanh hình chóp tam giác đều
Diện tích xung quanh của hình chóp tam giác đều được tính bằng tích của nửa chu vi đáy với trung đoạn.
Công thức: Sxq = p.d
Trong đó:
p là nửa chu vi đáy
d là trung đoạn của hình chóp tam giác đều. Trung đoạn là đường cao xuất phát từ đỉnh dóng xuống trung điểm của 1 cạnh.
- Diện tích toàn phần hình chóp tam giác đều
Diện tích toàn phần của hình chóp tam giác đều được tính bằng tổng diện tích xung quanh và diện tích đáy: Stp = Sxq + Sđáy
Vì vậy, để tính diện tích xung quanh và diện tích toàn phần của hình chóp tam giác đều, bạn cần biết độ dài trung đoạn, chu vi, và diện tích mặt đáy.
Công thức tính thể tích hình chóp tam giác đều
Xem thêm : Phản ứng hóa hợp là gì? Những phản ứng hóa hợp trong tự nhiên
Việc tính thể tích của một hình chóp tam giác đều đơn giản không kém so với hình chóp thông thường. Công thức cụ thể như sau:
V=1/3(S.h)
Trong đó:
- S là diện tích đáy
- h là chiều cao
Như vậy, bằng cách sử dụng công thức này, bạn có thể dễ dàng tính được thể tích của hình chóp tam giác đều một cách chính xác.
Vẽ Hình Chóp Tam Giác Đều Bằng 3 Bước Đơn Giản
- Bước 1: Bắt đầu bằng việc vẽ mặt đáy của hình chóp dưới dạng tam giác ABC. Không cần phải vẽ ba cạnh bằng nhau hoàn toàn, bạn có thể vẽ một tam giác thông thường. Chú ý AC vẽ dưới dạng nét đứt.
- Bước 2: Tiếp theo, vẽ hai đường trung tuyến CF và AI. Hai đường này sẽ gặp nhau tại một điểm O, và O sẽ là chân đường cao trùng với tâm của mặt đáy.
- Bước 3: Từ điểm O, hãy dựng một đường thẳng đứng. Đỉnh của hình chóp là điểm S, nối S với ba điểm A, B, C để hoàn tất việc vẽ hình chóp tam giác.
=> Sau khi hoàn thành, bạn sẽ có hình chóp tam giác đều SABC với đường cao SO và ba cạnh đáy SA, SB, SC bằng nhau.
Phân Biệt Các Loại Hình Chóp
Khi nghiên cứu về hình học không gian, việc phân biệt giữa các loại hình chóp là điều quan trọng để hiểu rõ hơn về đặc điểm và cấu trúc của chúng. Dưới đây là một số loại hình chóp phổ biến:
Hình Chóp Tam Giác Đều
- Đáy: Tam giác đều
- Mặt Bên: Tam giác đều
- Số Cạnh Đáy: 3
- Số Cạnh: 6
- Số Mặt: 4
Hình Chóp Tứ Giác Đều
- Đáy: Hình vuông
- Mặt Bên: Tam giác cân
- Số Cạnh Đáy: 4
- Số Cạnh: 8
- Số Mặt: 5
Hình Chóp Ngũ Giác Đều
- Đáy: Ngũ giác đều
- Mặt Bên: Tam giác cân
- Số Cạnh Đáy: 5
- Số Cạnh: 10
- Số Mặt: 6
Hình Chóp Lục Giác Đều
- Đáy: Lục giác đều
- Mặt Bên: Tam giác cân
- Số Cạnh Đáy: 6
- Số Cạnh: 12
- Số Mặt: 7
Với những thông tin trên, bạn có thể dễ dàng phân biệt giữa các loại hình chóp dựa trên các đặc điểm cụ thể của chúng.
Hình chóp tam giác đều là một trong những hình học không gian quen thuộc từ thời cấp 2. Bài viết dưới đây sẽ cung cấp định nghĩa, tính chất, công thức chu vi, diện tích và thể tích của hình chóp đều cùng với các dạng bài tập liên quan. Nếu bạn cần làm mới lại kiến thức về hình chóp tam giác đều, hãy tham khảo ngay.
Câu hỏi thường gặp
1. **Hình chóp là gì và đặc điểm của hình chóp?**
– Hình chóp là hình học không gian với mặt đáy là đa giác lồi và các mặt bên là các tam giác có chung một đỉnh.
2. **Hình chóp tam giác đều có những đặc điểm gì?**
– Hình chóp tam giác đều có mặt đáy là tam giác đều, các mặt bên đều là tam giác cân và bằng nhau.
3. **Tính chất nào đặc trưng cho hình chóp tam giác đều?**
– Hình chóp tam giác đều có 3 mặt phẳng đối xứng, mặt đáy là tam giác đều, các cạnh bên bằng nhau, và số đo góc tạo bởi các mặt bên và mặt đáy đều nhau.
4. **Công thức tính chu vi và diện tích hình chóp tam giác đều là gì?**
– Chu vi hình chóp là tổng chu vi mặt đáy và các mặt bên, diện tích bao gồm diện tích xung quanh và diện tích toàn phần.
5. **Làm thế nào để vẽ hình chóp tam giác đều bằng 3 bước đơn giản?**
– Bước 1: Vẽ mặt đáy là tam giác đều. Bước 2: Vẽ đường trung tuyến và chân đường cao. Bước 3: Nối các đỉnh để hoàn thiện hình chóp tam giác đều.
6. **Có những dạng bài tập nào phổ biến về hình chóp tam giác đều?**
– Xác định mối quan hệ giữa các yếu tố cạnh và mặt phẳng của hình chóp tam giác đều, và áp dụng kiến thức để giải các bài tập vận dụng.
Tóm tắt
Trong bài viết này, chúng tôi đã cung cấp cái nhìn tổng quan về hình chóp tam giác đều, bao gồm định nghĩa, tính chất, công thức tính chu vi, diện tích và thể tích. Đừng ngần ngại áp dụng kiến thức này vào thực hành và rèn luyện khả năng giải bài tập. Ghé thăm trang web để tìm hiểu thêm thông tin và hướng dẫn chi tiết.
Nguồn: https://laginhi.com
Danh mục: News
